|
Application
of the Falling Needle Viscometer
Application of the Falling
Needle Viscometer
Noh A. Park (1)
and T. F. Irvine, Jr. (2)
(1)
Stony Brook Scientific, Ltd., 1055 West Germantown Pike, Norristown, PA 19403
(2)
Mechanical Engineering Dept., State University of New York, Stony Brook, NY
11794
Introduction
The Falling Needle Viscometer (FNV) [1] was originally developed to
measure the rheological properties of Newtonian and non-Newtonian fluids.
However it is a versatile instrument and its functions have been expanded
to experimentally determine other physical properties.
These include, in addition to the liquid viscous properties, liquid
density, zero shear rate viscosity and yield stress, mixture concentration,
relative particle settling rates, intrinsic viscosity and molecular weight, high
pressure and high temperature viscosity, and time constant measurements of
viscoelastic fluids.
The operating principle of the FNV
is quite simple and is described in detail elsewhere [2, 3, 4 and 5] so only a
general description will be presented here.
Figure 1 shows a schematic of the instrument which consists of an inner
cylinder containing the liquid whose properties are to be measured.
A constant temperature liquid is circulated between the measuring
cylinder and the coaxial outer cylinder to specify the temperature of the test
liquid.
A slender hollow cylinder (needle) with
hemispherical ends and a weighted tip or a controlled needle with hemispherical
ends and extension bar plus external weights falls through the test liquid with
the longitudinal axes of the needle and the measuring cylinder parallel to the
gravity vector. The needle quickly
reaches its terminal velocity, which is then measured either visually or
electronically. A knowledge of the
terminal velocity, the fluid and needle densities, and the needle geometry is
sufficient to determine the viscous properties of the fluid.
The manufacturer (Stony Brook
Scientific, Ltd.) makes available three models of the falling needle viscometer.
The FNV-200 is a general laboratory model where the needle velocity is
measured by placing a small magnet in the needle tip which activates a pair of
Hall sensors located outside of the outer cylinder and which turn on and off a
digital clock (see Fig. 1). Partial
specifications are: viscosity range, 0.5 to 106 cP, absolute
accuracy, better than ±1%.
Model DV-100 is shown in Fig. 2 and has several additional features than
the FNV-200. An important feature is the fact that the measuring cylinders are
smaller and thus require less experimental fluid (4.5ml).
In addition, the measuring cylinders of the DV-100 are disposable which
does away with cleaning problems. Partial
specifications are: viscosity range, 1 to 108 cP, absolute accuracy,
better than ±1%.
For field work with a viscometer that doesn’t require the accuracy of
the other models, the PDV-100 is available. The absolute accuracy is better than
±5%
and the needle velocity depending on the needle density is measured either
visually or electronically.
In the following section, a number of possible FNV measurement techniques
are discussed.
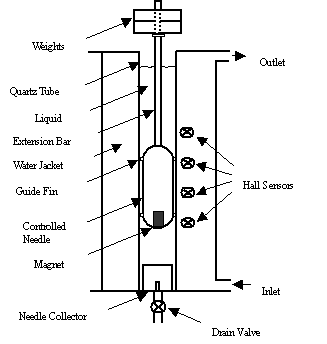
Figure
1 Schematic of falling/controlled needle viscometer

Figure
2 Photo of a DV-100 disposable viscometer with
microprocessor console
Applications
Newtonian
fluid viscosity measurements
Figure 3 shows the results of Newtonian fluid dynamic viscosity
measurements using the DV-100. The
process is described in Reference [3]. The
fluid is a standard viscosity fluid from the Cannon Instrument Co.
In the figure, the ordinate is the measured viscosity and the abscissa is
a number identified with a single measurement run. From the figure, the accuracy (as compared to the standard
fluid) is better than + 1% and the reproducibility is also better than +
1%.
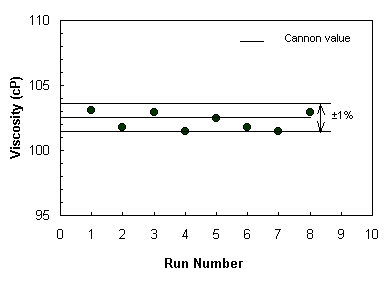
Figure
3 Viscosity measurement for Cannon S-60 fluid with
DV-100 disposable viscometer
Non-Newtonian
fluid viscosity measurements
The Falling Needle Viscometer can also be used to measure the rheological
properties of purely viscous non-Newtonian fluids. The process is described in Ref. [4]. Figure 4 shows the results of using the FNV to measure the
apparent viscosity vs. the shear rate for AP 273 Separan.
Also of interest in Fig. 4 are apparent viscosity measurements of the
same fluid using a commercial rotating cylinder viscometer (RCV).
It is seen that the agreement between the two methods is quite
satisfactory. It can also be noted
that the FNV can operate at much lower shear rates than the RCV (lowest shear
rate measured at 0.05RPM of the RCV, which is the low limit of the RCV).
This is important in measuring yield stresses, which will be discussed
below.
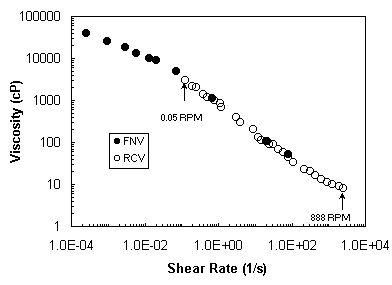
Figure
4 Typical flow curve measured with the Falling
Needle Viscometer (FNV) and Rotating Cylinder Viscometer (RCV), AP 273 Separan
2000 wppm at 25oC
Density and viscosity measurements
One of the advantages of the FNV is that for Newtonian and power-law
non-Newtonian fluids it is possible to measure the fluid density at the same
time as measuring the fluid viscosity. This
technique is described in Refs. [4], [6] and [7].
Essentially it involves dropping two needles of the same geometry but of
different densities. Figure 5 and 6
show the results of such measurements made on S-600 standard fluid along with a
comparison line taken from Cannon specifications. It is seen from the figure that the accuracy of the density
measurements is of the order of ±0.27%.
In addition to the above technique for measuring liquid densities, an
alternative method has recently been developed [7].
This method involves dropping three or more needles and has the
possibility of greater accuracy than the former method.
With the same data for calculating the liquid density, the viscosity can
also be obtained.
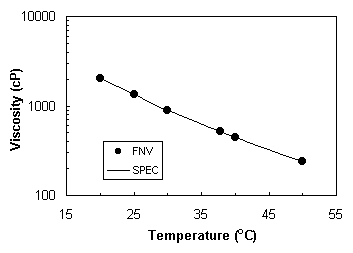
Figure 5 Viscosity measurement of Cannon S-600 standard
fluid
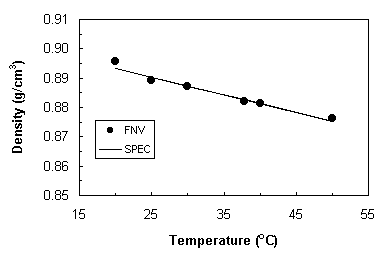
Figure
6 Density measurement of Cannon S-600 standard fluid
Zero shear rate viscosity
measurements
One of the important properties of non-Newtonian fluids is the zero shear
rate viscosity. Strictly speaking,
this is the value of the viscosity when the fluid is at rest and therefore
cannot be measured by any viscometer. The
method generally used is to measure the viscosity at lower and lower shear rates
and then extrapolate the resulting curve to zero shear rate.
Clearly, in using such a technique, the lower the shear rate at which
viscosities can be measured, the more accurate the extrapolation process.
As mentioned above, because the FNV is capable of viscosity measurements
at very low shear rates, it is particularly suitable for these zero shear rate
viscosity determinations. Examples
of such measurements are given in Ref. [4].
Yield
stress measurements
There is a class of fluids that when subjected to a stress do not go into
motion until a certain stress is applied. This
critical stress is called yield stress. It
is an important property for such liquids as paints which need to remain without
motion on a vertical surface until they dry, or medical ointments so that they
remain in place on the skin.
The FNV can be used to measure a yield stress as follows: Consider a
falling needle when the fluid has a yield stress [8].
If the density difference driving force (weight minus buoyancy) is
exactly equal to the yield stress force, the needle velocity will be zero and
the needle will be stationary. Under
these conditions, a simple force balance can be made between the yield stress,
weight and buoyancy force
typdL + typ2d2/4
= (rn
- rl)s
g (pd2L/4
+ pd3/6)
(1)
Where
ty = yield stress, d = needle
diameter, L= total needle length minus one diameter, (rn
-rl)s
= static density difference between needle (rn) and liquid (rl),
and g = acceleration of gravity. The second term on the left hand side is the net vertical
shear force around the two hemispherical ends.
Equation (1) states that if we can get the density difference just right,
the needle will be suspended at zero velocity.
This density difference is difficult to determine and an extrapolation
process is called for. The process
is illustrated in Fig. 7 where a number of needles of different densities were
dropped and their velocities measured. If
the solid line is extrapolated to zero velocity then the density difference at
that point is the proper one to insert into Equation (1) to calculate the yield
stress ty.
It should be noted that the lower the measured velocity in Fig. 7, the
more accurate the extrapolation process to obtain the critical density
difference. That is why the FNV is
especially appropriate for such measurements.
Also, yield stresses are often quite small (less than 0.1 N/m2)
which makes direct measurements very difficult.
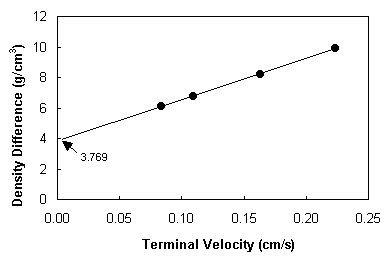
Figure 7 Yield stress measurement of ointment (density
difference: needle density minus liquid density)
Mixture
concentration measurements
The dynamic viscosity of liquid-liquid mixtures is sensitive to mixture
composition. This suggests that
viscosity measurements can be used to determine liquid concentrations for
homogeneous liquid-liquid mixtures. As
an illustration of such concentration measurements, Ref. [9] shows viscosity
measurements of small amounts of kerosene or gasoline mixed with motor oil at
different temperatures.
A
careful inspection of the figure in Ref. [9] would reveal that a 5%
concentration by weight of gasoline in oil at 20oC results in a 40%
change in viscosity as compared to pure motor oil. These measurements were made with the FNV which can therefore
serve as a concentration measuring device once properly calibrated for a given
liquid-liquid mixture.
Relative particle settling
rate measurements
Dynamic
viscosity changes are most sensitive to changes in liquid composition. This
makes it possible to test for contaminants in a liquid or to study the
sedimentation process of particles in a liquid.
In a study of the latter [9], viscosity measurements were made for
cornstarch, particles falling in distilled water.
Figure 8 shows the results of these measurements and illustrates the
technique for measuring the local needle velocity during its decent.
On the right side of Fig. 8 is a schematic of the FNV inner cylinder.
The H symbols stand for Hall sensors of which there are four.
Thus it is possible to measure their local needle velocities. These local falling velocities are plotted against the
falling distance in Fig. 8 with the parameter being the elapsed time from when
the aluminum particles-water mixture was made homogeneous by shaking.
For example, the horizontal line marked 0 minute indicates that just
after shaking the decent velocity was constant along the needle’s path.
The upper line marked solvent (distilled water) indicates the decent
velocities before the introduction of any aluminum particles.
The result of such an experiment is that one can deduce that all of the
significant settling has occurred during 100 minutes.
Another interesting conclusion is that the needle velocity distribution
never reaches that of the pure solvent (complete settling). This possibly indicates that the smallest particles, which do
not settle because of Brownian motion, continue to exert a significant influence
on the needle decent velocity.
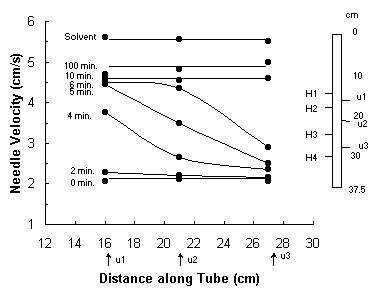
Figure 8
Needle velocity vs. distance along tube for 2% aluminum particles in distilled
water
Intrinsic viscosity and
molecular weight determination
Another FNV measurement technique is the measurement of the molecular
weight of a polymer by measuring the intrinsic viscosity of polymer solutions at
lower and lower concentrations. Such
a technique consists of measuring the viscosity of polymer solutions at lower
and lower polymer concentrations [10].
Such measurements have been made with the FNV and they compare favorably
with other techniques.
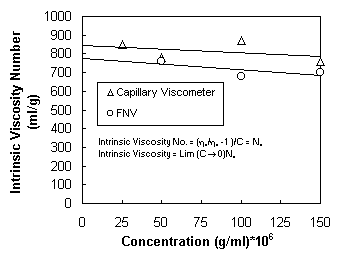
Figure 9
Intrinsic viscosity measurement of CMC polymer solution
High pressure
viscosity measurements
Viscosity measurements at pressure higher than ambient are of interest in
a number of fields such as oil recovery, polymer processing, etc. Such measurements are difficult however since the
experimental fluid must be isolated from its surroundings to allow independent
control of the fluid pressure level.
An atmospheric pressure falling needle viscometer has been converted to a
high pressure dynamic viscosity instrument.
The conversion is relatively straight forward since the only information
that must be transferred from the high pressure region to the surroundings is a
time signal which is transmitted via a magnetic pulse.
Using the FNV modified for high pressure operation, high pressure
viscosity measurements were made on Cannon S-600 oil over a pressure range of
1-110 atmospheres, as shown in Fig. 10 and described in Ref. [11].
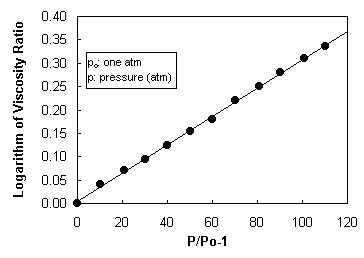
Figure 10
Variation of viscosity with pressure for Cannon S-600 oil
High temperature
viscosity measurements
Rheological property measurements at high temperature are very important
to characterize the molten plastics, pitches, asphalts, etc.
Such measurements are difficult however since the experimental sample
must be isolated from its surroundings to allow independent control of the
sample temperature.
A falling/controlled needle viscometer has been converted to a high
temperature viscosity instrument. The
conversion is relatively straight forward since the only information that must
be transferred from the high temperature region to the surroundings is a time
signal which is transmitted via a magnetic pulse.
Using the falling/controlled needle viscometer modified for high
temperature operation, high temperature viscosity measurements were made on Low
Density Polyethylene at 190oC as shown in Fig. 11.
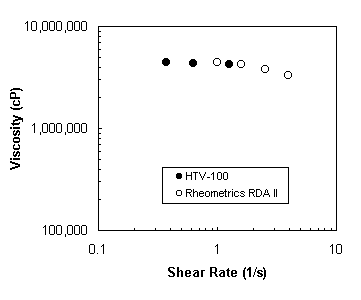
Figure 11
Viscosity measured by the high temperature viscometer compared to the data
measured by the Rheometrics RDA II for Low Density Polyethylene at 190oC
Time
constant measurements of viscoelastic fluids
It is well known that viscoelastic fluids possess a memory. If such a fluid is disturbed by changing its shear field from
equilibrium, only after a finite time will the fluid return to its original
equilibrium state. This time can be
characterized as a time constant for the fluid.
In a recent study [12], time constant measurements were made on a highly
viscoelastic fluid (Polyacrylamide Gel) using the falling needle viscometer
(model: DV-100). The procedure was
as follows. The viscoelastic fluid
was placed in the viscometer and temperature equilibrium was established.
Then, a needle was dropped and the time was measured for the needle to
fall a specified distance. This time called to was the reference time for a
needle to fall in an undisturbed fluid. Following
this measurement of t0, after a specified time, tp, had
passed, the same needle was dropped and the time, t, was measured.
This sequence was repeated with fresh fluid until a series of values of
t/t0 were obtained. The
same series of measurements were also made with different needle densities to
study the relaxation time of different stress fields.
The above measurements were displayed on a graph such as Fig. 12.
The figure shows that when the specified time interval, tp, is
small. The needle velocity is
smaller than the t0 run because of the flow disturbance caused by the
first needle drop. As tp
increases, t approaches t0 as the flow disturbance disappears.
In Fig. 12, the time constant for the heaviest needle is of the order of
65 minutes while it is only of the order of 15 minutes for the lighter needles.
A knowledge of these time constants make it possible to measure certain
fluid properties for viscoelastic fluids such as the steady shear viscosity
without running into elastic effects.
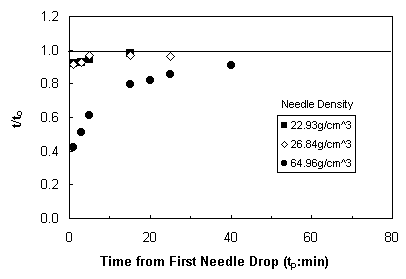
Figure 12
Time interval effects of three falling needles for Polyacrylamide Gel at 25oC
Summary and Conclusions
A brief discussion was presented of the operating principle of the
Falling Needle Viscometer. Then, a
series of viscometer applications were discussed including viscosity
measurements of Newtonian and purely viscous non-Newtonian fluids, liquid density, zero shear rate viscosity and yield
stress, mixture concentration, relative particle settling rates, intrinsic
viscosity and molecular weight, high pressure viscosity, high temperature
viscosity, and time constant measurements of viscoelastic fluids.
References
1.
ASTM D 5478-98, “Standard Test Methods for Viscosity of Materials by a
Falling Needle Viscometer”, Vol. 06.01, pp. 615-619 (2000)
2.
Park N.A., Measurement of rheological properties of non-Newtonian fluids
with the Falling Needle Viscometer, Ph.D. Thesis, State University of New York
at Stony Brook (1984)
3.
Park, N.A. and Irvine, T.F. Jr., “The Falling Needle Viscometer - A new
technique for viscosity measurements”, Warme und Stoffubertragung, Vol. 18,
pp. 201-206 (1984)
4.
Park, N.A. and Irvine, T.F. Jr., “Measurement of rheological fluid
properties with the Falling Needle Viscometer”, Rev. Sci. Instrum., Vol. 59,
9, pp. 2051-2058 (1988)
5.
Park, N.A. and Irvine, T.F. Jr., “A multipurpose Falling Needle
Viscometer to measure thermophysical properties of Newtonian and non-Newtonian
fluids”, American Laboratory News, pp. 8-9, December (1989)
6.
Park, N.A. and Irvine, T.F. Jr., “Liquid density measurements using the
Falling Needle Viscometer”, International Communications in Heat and Mass
Transfer, Vol. 20, pp. 303-312 (1997)
7.
Park, N.A. and Irvine, T.F. Jr., "An alternative method of
simultaneously measuring viscosity and density of Newtonian and power-law fluids
using the Falling Needle Viscometer ", Proceedings of the XIIIth
International Congress of Rheology, Cambridge, UK, Vol. 3, pp.140-142 (2000)
8.
Park, N.A., Irvine, T.F. Jr. and Gui, F., “Yield stress measurements
with the Falling Needle Viscometer’, Proceedings of the Xth International
Congress on Rheology, Sydney, Australia, Vol. 2, pp. 160-162 (1988)
9.
Park, N.A., Irvine, T.F. Jr. and Gui, F., “The use of the Falling
Needle Viscometer to determine liquid-liquid concentrations and particle
settling rates”, Proceedings of the First KSME and JSME Thermal and Fluids
Engineering Conference, Seoul, Korea, Vol. 2, pp. 256-259 (1988)
10. Park, N.A. and
Irvine, T.F. Jr., "Multifunctional Falling Needle Viscometer to measure
thermophysical properties of Newtonian and non-Newtonian fluids:
Applications", Surface
Phenomena and Additives in Water-Based Coatings and Printing Technology, edited
by M.K. Sharma, Plenum Press, New York, pp. 241-253 (1991)
11. Irvine,
T.F. Jr., Park, N.A., Gui, F. and Park, S.S., “A High Pressure Falling Needle
Viscometer”, Proceedings of the XIth International Congress on Rheology,
Brussels, Belgium, Vol. 2, pp. 985-987 (1992)
12. Park, N.A., Irvine T.F., Jr.
and Choi, B.G., “Time constant measurements of highly viscoelastic fluids with
the Falling Needle Viscometer”, Proceedings of the 3rd Pacific Rim
Conference on Rheology, Vancouver, July 8-13 (2001)
back
to top

|